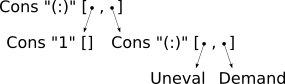
Repräsentation des Terms 1:!:_
Haskell has many advantages (e.g. laziness) which however, make finding bugs difficult. In imperative languages, debugging is simply possible using printf statements. In Haskell this is only possible using the unsafe function unsafePerformIO: [^ unsafe]
import System.IO.Unsafe (unsafePerformIO)
trace :: String -> a -> a
trace str x = unsafePerformIO $ do
putStr str
return xThe semantics of trace is the identity, but once the calculation of trace is triggered, the string is printed as a side effect:
ghci> trace "Hallo" (3 + 4)
Hallo 7
ghci> take 4 (map (trace "*") [1..])
[*1,*2,*3,*4]Often in debugging, you are also interrested in values:
traceAndShow :: Show a => a -> a
traceAndShow x = trace (show x) xghci> take 4 (map traceAndShow [1..])
[1 1,2 2,3 3,4 4]One problem is the mixture of dbug output and the result of the computation. This problem could be solved by using a seperate trace file. Another problem is the dependence of the output in relation to evaluation order, which may be quite confusing in the context of lazy-evaluation.
x = let l = map traceAndShow [1..] in sum (take 4 l)
y = let l = map traceAndShow [1..] in sum (reverse (take 4 l))ghci> x
1 2 3 4 10
ghci> y
4 3 2 1 10Further problems are:
traceAndShow partially destroys laziness: traceAndShow [1 ..] does not terminate as soon as it is triggered! Biside non-termination this can result in a loss of efficiency and also not work if the evaluation is suppossed to be lazy, like we did in some parser combiners.Show, e.g. no functions.The idee of Hood is to observe values like using traceAndShow, but delaying the output of the observation until the programm finishes (or is interrupted by pressing Strg-C). Furthermore, non-evaluated sub-structures are represented by "_". To distinguish the observations of a program, the user can add a string label:
ghci> :l Observe
ghci> take 2 (observe "List" [1..])
[1,2]
>>>>>>> Observations <<<<<<
List
----
(1 : 2 : _)
ghci> observe "List" [1,2,3,4,5]!!3
4
>>>>>>> Observations <<<<<<
List
----
(_ : _ : _ : 4 : _ : [])Usage: After importing the module Debug.Observe arbitrary expressions can be observed using the function observe :: Observable a => String -> a -> a. The whole observation can be started using the function runO :: IO a -> IO ().
It is possible to observe all data types (for own data types an instance of class Observable has to be defined, details can be found in the documentation of the library). Also functions can be observes. They are represented by the used part of their function graph:
ghci> map (observe "inc" (+1)) [1..3]
[2, 3, 4]
>>> Observations <<<
inc
---
{ \ 3 -> 4
, \ 2 -> 3
, \ 1 -> 2
}In practice, it is often more useful to observe functions instead of first order data structures, since they represent the functionality of your program. Let's consider a function definition of a function we want to observe:
f p_11 .. p_1n = e_1
...
f p_m1 .. p_mn = e_mTo observe all calls of f we can simply redefine the function as follows:
f = observe "f" f'
f' p_11 .. p_1n = e_1
...
f' p_m1 .. p_mn = e_mHence, all calls of F including the recursive once will be observed. This can result in too many observations. Therefore, it is often better to only observe the initial calls off`:
f = observe "f" f'
f' p_11 .. p_1n = e_1[f/f']
...
f' p_m1 .. p_mn = e_m[f/f']Beside this it is also possible to only observe some special calls of a function.
Furthermore, Hood allows
We start with the definition of a data type, which allows the representation of arbitrary data values. Our data type also contains representations for non-evaluated sub-expressions and demand requests, which show that an evaluation was initiated, but did not succeed to produce a head-normal-form (HNF) yet.
data EvalTree
= Cons String [EvalRef]
| Uneval -- entspricht '_'
| Demand -- entspricht '!', abgebrochene Berechnung
type EvalRef = IORef EvalTreeAn eample for a canceled computation is
ghci> observe "List" [1, fac (-1)]
[1,
<< Ctrl-C >>
>>> Observations <<<
List
----
(1:!:_)The computation of fac (-1) would not terminate and the is reflected by a started, unseccessful evaluation of the second list element, represented by an exclamation mark.
The representation of this observation result as en EvalTree is presented in the following figure:
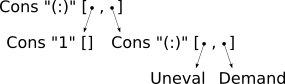
Repräsentation des Terms 1:!:_
The evaluation of a data value is usually represented in the following steps:
Uneval).Uneval by a Demand.Demand is replaced by a Cons containing the name of the constructor with a list of Unevals, representing the so fare non-evaluated subexpressions.Hence, we want to modify nodes within our EvalTree during the observed computation takes place. This will be organized as a side effect and we use IORefs for every node within the EvalTree, to make mutations of EvalTrees possible.
We start with a simple example data type, which we want to observe:
data Tree = Empty | Node Tree Tree
oTree :: Tree -> EvalRef -> Tree
oTree Empty ref = unsavePerformIO $ do
mkEvalTreeCons "Empty" ref 0
return Empty
oTree (Node tl tr) ref = unsafePerformIO $ do
[tlRef, trRef] <- mkEvalTreeCons "Node" ref 2
return (Node (oTree tl tlRef) (oTree tr trRef))
mkEvalTreeCons :: String -> EvalRef -> Int -> IO [EvalRef]
mkEvalTreeCons consName ref n = do
refs <- sequence $ replicate n $ newIORef Uneval
writeIORef ref (Cons consName refs)
return refsA lazy function, using this data type can be:
isNode (Node _ _) = True
isNode _ = FalseUsing our observer, we want to obtain:
ghci> isNode (observe "tree" (Node Empty Empty))
~> isNode (oTree ref (Node Empty Empty))
-- where ref points to:
-- Cons "Node" [ref1 ~> Uneval, ref2 ~> Uneval]We can generalize the apporach to arbitrary data types using the following class:
class Observe a where
obs :: a -> EvalRef -> a
instance Observe Tree where
obs = oTree
observer :: Observe a => a -> EvalRef -> a
observer x ref = unsafePerformIO $ do
writeIORef ref Demand
return (obs x ref)The function observe adds a Demand for every requestes sub-expression. If the sub-expression is evaluated to HNF, the function obs (here oTree) will convert this Demand into a Cons-value.
Furthermore, we sould correct the definition of oTree, such that also for the sub-observers, we call observe instead of oTree. The order should always be as follows:
\[\text{Uneval } \xrightarrow{\text{Request of the HNF}} \text{Demand } \xrightarrow{\text{HNF was computed}} \text{Cons}\]
To store all observations, we use a global constant:
global :: IORef [IO ()]
global = unsafePerformIO (newIORef [])
observe :: Observe a => String -> a -> a
observe label x = unsafePerformIO $ do
ref <- newIORef Uneval
modifyIORef global (showInfo ref :)
return (observer x ref)
where
showInfo ref = do
putStrLn (label ++ "\n" ++ replicate (length label) '-')
showEvalTreeRef ref >>= putStrLn
runO :: IO () -> IO ()
runO act = do
writeIORef global []
catch act (\e -> putStr "Runtime Error: " >> print (e :: SomeException))
printObs
printObs :: IO ()
printObs = do
putStrLn ">>> Observations <<<"
readIORef global >>= sequence_Now, it only remains to define a the function showEvalTreeRef, which converts EvalTrees into a user friendly String representation:
showEvalTreeRef :: EvalTreeRef -> IO String
showEvalTreeRef ref = readIORef ref >>= showEvalTree
showEvalTree :: EvalTree -> IO String
showEvalTree Uneval = return "_"
showEvalTree Demand = return "!"
showEvalTree (Cons cons []) = return cons
showEvalTree (Cons cons rs) = do
args <- mapM showEvalTreeRef rs
return $ "(" ++ unwords (cons : args) ++ ")"For arbitrary construcors, e.g. tuples or lists, it is also possible to define more readable representations, which can be done as an exercise.
So fare, it is not so trivial to define an Observe instance for own data types. However, comparing such instances, we can see, that all definitions are very similar and we can define auxiliar functions for constructors of a fixed arity:
instance Observe a => Observe [a] where
obs (x:xs) = o2 (:) "(:)" x xs
obs [] = o0 [] "[]"Here, the predefined observers for a given arity can be defined as:
o0 :: a -> String -> EvalRef -> a
o0 cons consName ref = unsafePerformIO $ do
mkEvalTreeCons consName ref 0
return cons
o2 :: (Observe a, Observe b)
=> (a -> b -> c) -> String -> a -> b -> EvalRef -> c
o2 cons consName vA vB ref = unsafePerformIO $ do
[aRef, bRef] <- mkEvalTreeCons consName ref 2
return $ cons (observer vA aRef) (observer vB bRef)As a next step, we implement the observation of functions. Similar to lazy data structures, functions are observed by representing the used part of their function graph. Arguments and return values are data which is also observed, like implemented above:
> map (observe "inc" (+1)) [3,4,5]
[4,5,6]
>>> Observations <<<
inc
---
{ \ 3 -> 4
, \ 4 -> 5
, \ 5 -> 6
}Note: Here, (+1) is a constant and the corresponding observer is only computed once, which means that we see three elements of its function graph. Realizing this similar to data constructors, we would override one aplication of a function by its next application. The solution is extension of the EvalTree with a special constructor Fun. In contrast to Cons it contains a list as its argument. Within this list we store all applications of the function. One application is represented as a pair of the observations of the argument and the result.
data EvalTree
= Cons String [EvalRef]
| Uneval
| Demand
| Fun [(EvalRef, EvalRef)]For the inc example from above, we obtain the following representation1:
Fun [ (Cons "3" [], Cons "4" [])
, (Cons "4" [], Cons "5" [])
, (Cons "5" [], Cons "6" [])
]The implementation is possible in a similar way as for algebraic data types:
instance (Observe a, Observe b) => Observe (a -> b) where
obs f ref x = unsafePerformIO $ do
applRefs <- readIOFunRef
argRef <- newIORef Uneval
resRef <- newIORef Uneval
writeIORef r $ Fun ((argRef, resRef) : applRefs)
return $ observer (f $ observer x argRef) resRef
where
readIOFunRef = do
v <- readIORef ref
case v of
Fun applRefs -> return applRefs
_ -> do
writeIORef ref (Fun [])
return []
showEvalTree :: EvalTree -> IO String
showEvalTree ...
showEvalTree (Fun appls) = do
resDStrs <- mapM showApp (reverse appls)
return $ unlines resStrs
where
showApp (rArg,rRes) = do
arg <- showEvalTreeRef rArgs
res <- showEvalTreeRef rRes
return $ concat ["{", arg, "->", res, "}"]Here we keep the output simple. This can however be improved:
ghci> observe "(+)" (+) 3 4
7
>>> Observations <<<
(+)
---
{3->{4->7}}Instead of using a EvalTrees for storing observations, it is also possible to store the debug information within a file. For presenting the observations, it is then possible to analyse the file at the end of the execution and and present these to the user. The opetunity is, that less memory is needed during the execution, the file contains additional information about the order in which the observations are constructed, although so fare no tool presents this order.
The presented approach is based on the implementation of Hood. There are further approaches for debugging, wich usually work as a program transformation and are in most cases only available for Haskell'98.
The advantage of Hood is, that it is light weight and relatively robust against language extensions. A disadvantage is, the fact that you usually do not obtain relations between different observations in Hood. Here approaches like Hat are more powerfull.
For a clearer understanding, we omit the references here.↩