Indexes within a functional array
In this chapter we discuss the implementation of selected data structures in Haskell. We have already discussed different techniques for efficiently working with lists as well as search trees for representing sets of comparable elements.
Lists essentially correspond to the stack abstraction as the following stack implementation illustrates:
type Stack a = [a]
emptyStack :: Stack a
emptyStack = []
isEmptyStack :: Stack a -> Bool
isEmptyStack = null
push :: a -> Stack a -> Stack a
push = (:)
top :: Stack a -> a
top = head
pop :: Stack a -> Stack a
pop = tailAll defined operations have constant runtime. Closely related with stacks are queues. While stacks work by last-in-first-out principle (LIFO), queues work by first-in-first-out principle (FIFO). The elements of a queue are therefore taken in the order in which they were inserted.
A simple implementation in Haskell can be realized as follows:
type Queue a = [a]
emptyQueue :: Queue a
emptyQueue = []
isEmptyQueue :: Queue a -> Bool
isEmptyQueue = null
enqueue :: a -> Queue a -> Queue a
enqueue x q = q ++ [x]
next :: Queue a -> a
next = head
dequeue :: Queue a -> Queue a
dequeue = tailLike the operations top and pop also next and dequeue have constant runtime, independent of the size of the queue. But the runtime of enqueue is linear, because the++ function is applied to the list representing the queue. If we turn the list representation to reverse order, we can implement enqueue in constant time, but need linear runtime in the size of the queue for next anddequeue, which is even worse.
Can we specify an implementation of queues that allows both enqueue as well asnext and dequeue in constant runtime? To allow access at both ends of the list, we can represent the queue using two lists, such that we can dequeue at the head of the first list and enqueue at the head of the other list:
data Queue a = Queue [a] [a]
emptyQueue :: Queue a
emptyQueue = Queue [] []
isEmptyQueue :: Queue a -> Bool
isEmptyQueue (Queue xs ys) = null xs && null ysThe first list contains the oldest elements, i.e. those that are dequeued next. The second list contains the newest elements, i.e. the ones that were inserted last, hence is in reverse order. Therefore, a new element can be added to the head of the second list. To remove an element, we take it from the first list.
enqueue :: a -> Queue a -> Queue a
enqueue x (Queue xs ys) = Queue xs (x:ys)
next :: Queue a -> a
next (Queue (x:_) _) = x
dequeue :: Queue a -> Queue a
dequeue (Queue (_:xs) ys) = Queue xs ysThe implementations of next anddequeue are still incomplete. Neither function gives a result if the first List is empty, but the second is not. This case would require to pass the second list completely and and access or remove the last element of the second list.
In order to avoid this unfavorable case, we create an invariant for the Queue data type:
If the first list is empty, the second one is empty, too.
If this invariant applies, we will always find the element to be removed from dequeue within the first list, since it always contains an element if the second list is non-empty.
Unfortunately, the implementations of enqueue anddequeue shown above do not maintain this invariant: after inserting an element in an empty queue, the first list is empty, but the second is not empty. This situation also occurs when the first list has one element before calling dequeue.
We therefore implement a constructor function queue that guarantees that the second list is empty if the first is empty:
queue :: [a] -> [a] -> Queue a
queue [] ys = Queue (reverse ys) []
queue xs ys = Queue xs ysBecause the items in the second list are in reverse order we have to reverse the second list before we can use it as the new first list. With the queue function we can redefine enqueue anddequeue as follows:
enqueue :: a -> Queue a -> Queue a
enqueue x (Queue xs ys) = queue xs (x:ys)
dequeue :: Queue a -> Queue a
dequeue (Queue (x:xs) ys) = queue xs ysUnlike the previous definitions, we use the queue function instead of the Queue constructor in the right hand-side of the rules. Due to the invariant, it is now sufficient to only check whether the first list is empty:
isEmptyQueue :: Queue a -> Bool
isEmptyQueue (Queue xs _) = null xsThe implementation of the next function is now correct because the invariant prevents the second list from containing elements when the first list is empty.
Despite calling queue inenqueue, enqueue has constant runtime: the potentially expensive call of reverse only happens if the first list xs is empty, and in that case because of the invariant also ys is empty. So the argument ofreverse a singleton.
In the worst case, the runtime of dequeue is still linear in the number of elements (\(n\)) within the queue: if the first list contains a single element and the second list contains \(n-1\) elements, the queue call performs \(n-1\) steps (due to the reverse call). This case occurs, for example, when \(n\) elements are added to an empty queue in a row with enqueue.
In comparison to the first implementation with only one list, did we gain anything at all? The pessimal runtime of dequeue is linear, but the amortized runtime of the two operations enqueue and dequeue is constant.
With an amortized runtime, one does not consider the term of one single operation but the runtime of multiple operations in a row: If any \(n\) queue operations in a row are executed and the total runtime is always in \(O(n)\), then the amortized running time of the operations is constant. The individual calls to the operations can have a worse runtime as long as the total runtime is never affected.
As an example we consider the following operations:
dequeue
(dequeue
(dequeue
(enqueue 1
(enqueue 2
(enqueue 3 emptyQueue)))))With the simple implementation we get
dequeue
(dequeue
(dequeue
((([] ++ [3]) ++ [2]) ++ [1])))Since ++ is applied from left to right, the total runtime is quadratic in the number of the added elements and hence quadratic in the number of used operations. Hence, the the amortized runtime of the two queue operations is linear, because \(n\) applications of an operation with a linear runtime leads to a quadratic runtime in total. The amortized duration of the operations is not better than that pessimal.
Now, let's look at the same example with the second Queue implementation (the result is shortened a bit):
deq (deq (deq (enq 1 (enq 2 (enq 3 e)))))
= deq (deq (deq (enq 1 (enq 2 (q [] [3])))))
= deq (deq (deq (enq 1 (enq 2 (Q [3] [])))))
= deq (deq (deq (enq 1 (Q [3] [2]))))
= deq (deq (deq (Q [3] [1,2])))
= deq (deq (q [] [1,2]))
= deq (deq (Q [2,1] [])) -- expensive!
= deq (Q [1] [])
= Q [] []The total runtime of these calls is linear in the number of operations because almost all steps have a constant runtime. Just one step has a linear runtime, but the total runtime remains linear in the number of operations. Therefore the amortized runtime of one operation (other than the pessimal term) is constant.
This chain of calls shows that the expensive reverse call only rarely occurs. In general, every element inserted must "once pass through" reverse before it is removed again. The reverse calls are so rare that the total runtime of any sequence of queue operations has linear total runtime.
Although the pessimal runtime of dequeue is linear, this queue implementation is due to the constant amortized runtime of operations very useful in practice.
Arrays are a common data structure in many imperative programming languages. Imperative arrays allow access to and manipulation of elements at a given position with usually constant runtime. Haskell provides a arrays within the module Data.Array. These arrays allow access to the element at a given position in constant time and the construction of an array from a given list in linear time in the size of the array. However, the operation to change an index has linear runtime. It copies the entire array because side effects are not allowed in the pure functional language Haskell. In particular also the old array has to be available unchanged after performing an update operation.
Can we also implement arrays with constant runtime in a purely functional language? An approach can be the following data type:
data Array a = Entry a (Array a) (Array a)We first notice that all values of this type are infinite, since there is no case for the empty array.
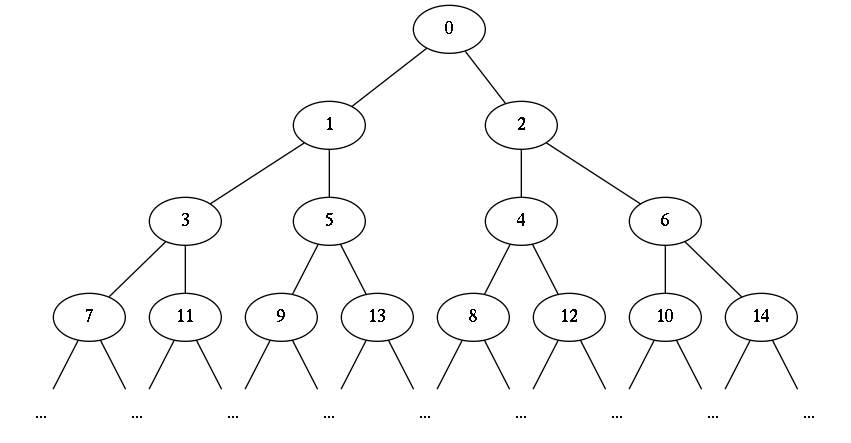
Indexes also do not occur within the array data type. The idea of this implementation is that the particular index is implemented as a path within the tree leading to the selected entry. For example, the element with the index zero can be found at the root. The left subtree contains all elements with an odd index and the right subtree contains elements with an even index. The partial arrays in turn have the same structure: you decrement the indexes and divide the result (with integer Division) by two. Again the index zero is in the root, odd values are in the left tree and even values in the right. Overall, this results in the following index distribution of the indexes:

Indexes within a functional array
This distribution allows an efficient access to all element as follows:
(!) :: Array a -> Int -> a
Entry x odds evens ! n
| n == 0 = x
| odd n = odds ! m
| even n = evens ! m
where
m = (n-1) `div` 2If the index is zero, the element is in root position. Otherwise, we descend in the left or right subtree in dependence of the index being odd or even. The next index is obtained by decrementing and bisecting the given index.
To access the element in position 9 we descend into the left subtree since 9 is odd. The next index is \((9-1)/2 = 4\). This value is even and we descend into the right subtree and compute the next index as \((4-1)/2 = 1\). Again this index is odd and we descend to the left subtree. Now we are done, since \((1-1)/2 = 0\) and find the value in this entry.
The function for modifying an entry can be implemented in the same way:
update :: Array a -> Int -> a -> Array a
update (Entry x odds evens) n y
| n == 0 = Entry y odds evens
| odd n = Entry x (update odds m y) evens
| even n = Entry x odds (update evens m y)
where
m = (n-1) `div` 2When descending the array, we construct a new array which contains the modified entry. In contrast to arrays in imperative languages the original array is still available. However, not the whole array is copied (like cloning in imperative languages). Only the path to the modified entry is copied. All other subtrees are shared between the two arrays.
The runtime of the functions (!) and update are logarithmic in the index. Hence, they are independent of the size of the array. To be honest, also in imperative languages the array access is not constant, but logarithmic in the index, since all (logarithmically many) bits of the index must be considered to find the addressed element.
The advantage of function arrays is, that both the new and the modified variant of an array are available and both are provided with logarithmic memory consumption in the size of the index. In imperative arrays you usually clone your array in this case, which means additional linear memory consumption, since the whole array is copied.
As we already mentioned in the beginning, all values of type Array a are infinite. It remains the definition of an empty array. The empty array is simply an infinite array only containing error messages:
emptyArray :: Array a
emptyArray = Entry err emptyArray emptyArray
where
err = error "accessed non-existent entry"A list can be converted into an array by successively adding the elements:
fromList :: [a] -> Array a
fromList = foldl insert emptyArray . zip [0..]
where
insert a (n,x) = update a n xThe runtime of fromList is \(O(n * log~n)\). However, in this implementation we construct many Entry nodes, which are in the next step directly replaced again. The following implementation avoids this by dividing the input list into two parts, the ones with odd respectively even index.
fromList :: [a] -> Array a
fromList [] = emptyArray
fromList (x:xs) =
Entry x (fromList ys) (fromList zs)
where (ys,zs) = split xsThe split function adds the elements alternately to these two lists:
split :: [a] -> ([a],[a])
split [] = ([],[])
split [x] = ([x],[])
split (x:y:zs) = (x:xs,y:ys)
where (xs,ys) = split zsAlso this variant has runtime \(O(n * log~n)\),but it does not produce superfluous Entry nodes and hence is much faster. It is also possible to provide fromList with linear runtime (Okasaki '97).
The presented implementation, with a further optimization (which we do not focus here), is available as module Data.IntMap.
In contrast to lists, arrays allow an efficient access to an element in an arbitrary position. On the other hand, lists allow efficient operations for adding and removing elements at the beginning of the list. The functions (:) and tail woul have linear runtime for our array representation, since we would have to move all elements of the array to another index.
Array lists provide as well an efficient access to arbitrary positions as well as deleting or adding elements at the top of the datastructure. Their internal representation is similar to binary numbers and encodes the binary representation of the length of the list. For every one in the binary representation, the array list contains a complete, leaf labeled tree of height corresponding to the position. For a zero bit, there is no tree.
Here are some examples of array lists up to length five:
0
|
5
0-----1
/ \
4 5
1-----1
| / \
3 4 5
0-----0-----1
/ \
/\ /\
2 3 4 5
1-----0-----1
| / \
1 /\ /\
2 3 4 5So an array list of length \(n\) contains information exactly in the positions, in which the binary representation of the size contains the bit one, starting with the least significant bit and ending with the highest bit (which will alwys be a one, since we avoid leading zeros). The binary tree in position \(i\) exactly contain \(2^i\) elements. Hence, from least significant bit to highest significant bit the trees contain twice as many elements as the previous tree (if it is available at all).
In sum all present trees contain as many entries as the length of the list expects.
A tree like
1-----0-----0
|
7is not allowed, since 001 is no valid binary number. Specifying correct array lists, we obtain the following invariants:
This representation allows all mentioned operations to be implemented in logarithmic runtime in the maximum of the sice of the tree or the given index.
We represent array lists as values of the following data type:
type ArrayList a = [Bit a]
data Bit a = Zero | One (BinTree a)
data BinTree a = Leaf a
| BinTree a :+: BinTree aThe empty array list is the empty list. We here avoid the notation from binary numbers, which would be 0.
empty :: ArrayList a
empty = []Thanks to the first invariant the test for emptyness can then be realized by checking whether the list is empty.
isEmpty :: ArrayList a -> Bool
isEmpty = nullAs a next step we want to define a function (<:) for array lists, which behave similar to (:). The length of the list will be extended by one and hence this operation relates to incrementing binary numbers. In this process you always have to consider a carry bit, which flips ones to zeros until you reach either a zero or the highes significant bit. In the last case, we add a new bit tor our array list, i.e. the array list was extended to length of a power of two.
(<:) :: a -> ArrayList a -> ArrayList a
x <: l = cons (Leaf x) lTo implement this incrementation we use an auxiliary function cons on binary trees, which also combines the trees along the one bits to successively growing binary trees:
cons :: BinTree a -> ArrayList a -> ArrayList a
cons u [] = [One u]
cons u (Zero : ts) = One u : ts
cons u (One v : ts) = Zero : cons (u :+: v) tsHence, reaching a zero or the new highest bit, we add the sucessively constructed tree. Furthermore the original Ones are converted to Zeros. The invariants are kept, since every recursive call is performed with a tree of double size. Note, however, that the trees are neither copied nor traversed. The runtime for cons is therefore restriced by the length of the initial ones within the binary numbers, which is in worst case the logarithm of the length of the array list.
The following example shows the successive extension of an array list:
ghci> 3 <: empty
[One (Leaf 3)]
ghci> 2 <: it
[Zero,One (Leaf 2 :+: Leaf 3)]
ghci> 1 <: it
[One (Leaf 1),One (Leaf 2 :+: Leaf 3)]To avoid name conflicts, we define functions hd and tl, which correspond to head and tail for lists. We realize both functions with a single auxiliary function, which computes both results in parallel. In the lazy language Haskell, only the relevant part will be computed.
hd :: ArrayList a -> a
hd l = x
where (Leaf x, _) = decons l
tl :: ArrayList a -> ArrayList a
tl l = xs
where (_, xs) = decons lThe function decons works similar to cons. It decrements the binary number and in parallel decomposes the binary tree in the first position containing a One entry. Since, for instance 0011 is converted into 1101, the tree in position 2 (we start counting positions with zero), which contains 4 entries is deconstructed into its right and left subtrees. The right subtree (containing two elements) is stored in position one and the left subtree is further deconstructed. So the right child of the left subtree is stored in position zero while the left child of the left child is returned as the hd element.
decons :: ArrayList a -> (BinTree a, ArrayList a)
decons [One u] = (u, [])
decons (One u : ts) = (u, Zero : ts)
decons (Zero : ts) = (u, One v : ws)
where
(u :+: v, ws) = decons tsThe first rule guarantees the invariant that the last element of the list is non-zero. Also the other invariants are guaranteed. The implementation in general is build on the invariant beeing valid. Otherwise the pattern matching i the where claus on a non-empty tree (u :+: v) could fail. Also the pattern matching in the defintion of hd cannot fail because of the invariant.
The runtime of decons and also of hd and tl are restricted by the number of bits, in other words by the logarithm of the number of elements within the array list. An examplke call of decons for an array list of length four looks as follows:
decons 0-----0-----1
/ \
/\ /\
1 2 3 4
let (u :+: v, ws) = decons 0-----1
/ \
/\ /\
1 2 3 4
in (u, One v : ws)
let (u :+: v, ws) =
let (u' :+: v', ws') = decons 1
/ \
/\ /\
1 2 3 4
in (u', One v' : ws')
in (u, One v : ws)
let (u :+: v, ws) =
let u' :+: v' = 1
/ \
/\ /\
1 2 3 4
ws' = []
in (u', One v' : ws')
in (u, One v' : ws')
let u :+: v = 1
/ \
1 2
ws = [One 1 ]
/ \
3 4
in (u, One v : ws)
(1, 1-----1 )
| / \
2 3 4As a next step, we define functions for accessing and manipulation elements at a given index. Similar to arrays an element can be accessed by the operator (!).
(!) :: ArrayList a -> Int -> a
l ! n = select 1 l nWe use an auxiliary function select, which takes the size of the next binary tree as an additional argument.
select :: Int -> ArrayList a -> Int -> aThis size will by doubled in every recursive call. If the actual bit is zero, we simply stepp the the next element within the list.
select size_t (Zero : ts) n =
select (2*size_t) ts nIf it is one, we decide in dependence of the size of the actual subtree, whether we find the element within this subtree or within the remaining list structure. In the latter case, we subtract the number of elements within the passed binary tree from the index.
select size_t (One t : ts) n
| n < size_t =
selectBinTree (size_t`div`2) t n
| otherwise =
select (2*size_t) ts (n-size_t)For the case, that we know, that the index belongs to the actual BinTree we decend into this tree with th same idea. The size parameter now represents the size of the left subtree. If this is larger than the index we decend into the left subtree. Otherwise we decend into the right subtree and subtract the number of elements within the left subtree from the index.
Whenever we decend in the full binary tree, we devide the size parameter by two.
selectBinTree :: Int -> BinTree a -> Int -> a
selectBinTree 0 (Leaf x) 0 = x
selectBinTree size_u (u :+: v) n
| n < size_u =
selectBinTree (size_u `div` 2) u n
| otherwise =
selectBinTree (size_u `div` 2) v (n-size_u)It is important,that all invariants hold. Otherwise the size parameters would not fit to the size of the corresponding trees.
The runtime of select is also restricted by the logarithm of the length of the array list. However, in many cases the element will already be found in logarithmic time with respect to th index.
As a last step we implement a function modify for modifying element at a given index. In additon to the index we pass a function parameter which modifies the element at thegiven index.
modify :: Int -> (a -> a) -> ArrayList a -> ArrayList a
modify = update 1The structure is similar to select. Additionally, we pass the update function and reconstruct the data structure around the modified value on the right hand side of each rule.
update size_t n f (Zero : ts) =
Zero : update (2*size_t) n f ts
update size_t n f (One t : ts)
| n < size_t =
One (updateBinTree (size_t`div`2) n f t):ts
| otherwise =
One t : update (2*size_t) (n-size_t) f ts
updateBinTree 0 0 f (Leaf x) = Leaf (f x)
updateBinTree size_u n f (u :+: v)
| n < size_u =
(updateBinTree (size_u`div`2) n f u) :+: v
| otherwise =
u :+: (updateBinTree
(size_u`div`2) (n-size_u) f v)The runtime of update is similar to select which is logarithmic in the length of the list. Only the path to the index is copied, the other parts of the data structure are shared.
We complete our interface with a function for converting lists into array lists, which is simply possible by means of foldr:
fromList :: [a] -> ArrayList a
fromList = foldr (<:) emptyAnalysing this function, on a first view the runtime seems to be in \(O(n \cdot \log n)\), where \(n\) is the length of the list, because every application of (<:) is in worst case logarithmic in the size of the so fare constructed array list.
However, this is too pessimistic. For every worst step case in the application of (<:), there are many many cheaper steps, before again an expensve stepp takes place. In the lecture we discussed, that each step in this construction of the array list has an amortized runtime of 2, which means is constant and the runtime of the function fromList is linear in the length of the list.
Although we have endeavored to keep the invariants within our first implementation, it is in general not trivial to guarantee this invariant. Beside proving formal correctness, it can by useful to specify the invariant and use QuickCheck to check these invariants.
isValid :: ArrayList a -> Bool
isValid l = (isEmpty l || nonZero (last l))
&& all zeroOrComplete l
&& and (zipWith zeroOrHeight [0..] l)Each line relates to the corresponding invariant. The first line expresses that the array list is either enpty or the higher bit is one. The second line expressed that every occuring binary tree is complete and the last line checks that each of these complete trees has a correct height. The implementation of the auxiliary functions is simple and presented in the lecture.
After defining QuickCheck generators for array lists, we can automatically test whether our implementations are correct. All presented function are correct, but it's quite easy to make a mistake implementing the funcions.
For instance, the following rule for cons seems to be correct on the first sight:
cons u (One v : ts) = cons (u :+: v) tsSimilarly, we we could make a mistake in the defintion of decons:
decons (One u : ts) = (u, ts)QucikCheck finds these bugs. But it would be nicer, if the type system would guarantee that we cannot construct an array list which does not fulfil all invariants. On a first sight it is not clear, how we can express such complex invariantes within Haskells type system. But it is possible.
We start with a simple idea, which will later help us guaranteeing the first invariant. Therefore, we define a variant of lists which cannot be empty.
data NEList a = End a | Cons a (NEList a)The other invariants are more complicated. We define a data type TreeList which guarantees all invariants for the elements. Its implementation reuses the idea of non-empty lists. furthermore, we encode a complete binary tree as nested pairs of the corresponding height.
For instance a full binar tree of height two resp. three (containing the elements from 1 to 4 resp. 8) can be represented by the nested pair:
((1,2),(3,4))
(((1,2),(3,4)),((5,6),(7,8)))Note, that however, each of these values has a different type. However, we can guarantee, that with each element within the list, we increase the type to another pair of two values of the last type:
data ArrayList a = Empty
| NonEmpty (TreeList a)
data TreeList a = Single a
| Bit a :< TreeList (a,a)Note, that Treelist a can either be a Single a representing the highest bit and also representing the non-empty end of the list. As an alternative, it can also be a recursive list, containing at least two elements, represented by the constructor (:<) . In this case, the first element is a value of type a and the tail is a TreeList (a,a), which means that a value in the next position has a different type. It is a pair nested one more in depth.
I remains to define the data type Bit, which is simply a variatin of the data type Maybe:
data Bit a = Zero | One aNow we can construct the following values of type TreeList Int:
Single 1
Zero :< Single (2,3)
One 1 :< Zero :< Single ((2,3),(4,5))But trying to define an array list wich does not respect the invarinates will result in a type error message at compile-time:
ghci> Zero :< Single (42 :: Int)
Couldn't match expected type `(a, a)'
against inferred type `Int'Changing the argument of a defined type constructor on the right hand-side of its definition is called 'nested data type'.
The functions for array lists can be transfered to the new data representation as follows:
The empty array list is represented by Empty:
empty :: ArrayList a
empty = Empty
isEmpty :: ArrayList a -> Bool
isEmpty Empty = True
isEmpty _ = FalseTo add an element to the front, we define a function (<:). Now we consider the case for the empty list seperately:
(<:) :: a -> ArrayList a -> ArrayList a
x <: Empty = NonEmpty (Single x)
x <: NonEmpty l = NonEmpty (cons x l)The function cons is again defined like incrementing a binary number:
cons :: a -> TreeList a -> TreeList a
cons x (Single y) = Zero :< Single (x,y)
cons x (Zero :< xs) = One x :< xs
cons x (One y :< xs) = Zero :< cons (x,y) xsHowever, when we decend in the list, we respect the different nesting of pairs before and after the constructor (:<). If we now forget an entry within the bit list, for instance the part Zero :< in the last rule, then we obtain a type error, like the following:
Occurs check:
cannot construct the infinite type:
a = (a, a)Note the recursive call to cons in the last rule. Its first argument is of type (a,a) and the list xs is of type TreeList (a,a). If the type of a recursive function differs from the type of its definition, then this is called polymorphic recursion. This is usually necessary, when we use non-regular data types, in other words when implementing functions for nested data tyes.
The type of a polymorphic recursive function1 cannot be infered. the type signature of cons can therefore not be omitted. Compiling the code without the type information for cons results in a type error similar to the one above.
Similar we can define hd and tl by means of an auxiliar function decons, which computes both results in parallel.
hd :: ArrayList a -> a
hd (NonEmpty (Single x)) = x
hd (NonEmpty l) = fst $ decons l
tl :: ArrayList a -> ArrayList a
tl (NonEmpty (Single _)) = Empty
tl (NonEmpty l) = NonEmpty . snd $ decons ldecons is never called with a one elemnt list, which relates to decrementing natural number larger than one.
decons :: TreeList a -> (a, TreeList a)
decons (One x :< xs) = (x, Zero :< xs)
decons (Zero :< Single (x,y)) = (x, Single y)
decons (Zero :< xs) = (x, One y :< ys)
where ((x,y),ys) = decons xsSince in every call of decons, the case for the one elemantry list is handled, this implementation of decons is safe. Again we would obtain type error messages, if we violate the invariant.
Accessing an element in a given position gets more complicated, since we have to consider the changing nesting of pairs, when decending in the list. We cannot us simple recursion for this as before.
A possible solution to this problem is the introduction of an additional selection function, which accesses the correct element within the nested pair structure. The type of this function can then be changed when decending within the list structure. The initial function can be defined on top level in the definition of (!). Although the selection function will later be modified during recursion, we can here give a good error message using the parameter n:
(!) :: ArrayList a -> Int -> a
Empty ! _ = error "ArrayList.!: empty list"
NonEmpty l ! n = select 1 sel l n
where
sel x m
| m == 0 = x
| otherwise =
error $ "ArrayList.!: invalid index "
++ show nIn the auxiliary function select we now have another parameter del, which will change in type from one recursion to the next. This function directly selects the expected element from the nested pair structure. In the first call the function sel has the type a -> Int -> a, which however changes within the recursive call to (a,a) -> Int -> a and ((a,a),(a,a)) -> Int -> a in the next call and so on. We generalize all these calls by the more general type (b -> Int -> a) for an arbitrary selection funtion. In parallel also the type of the TreeList we work on changes an we obtain:
select :: Int
-> (b -> Int -> a)
-> TreeList b -> Int -> aIn the definition, we first handle the base case:
select _ sel (Single x) n = sel x nHere it is now possible to ignore the size parameter. The function sel performes the selection and we can avoid the complicated calculation from our first implementation.
The second rule uses the size parameter similar like the first implementation. However, it constructs a new selection function, called descend, which performs the navigation within the full binary tree, where the index we are lookuing for is located.
select size_x sel (bit :< xs) n =
case bit of
Zero -> select (2*size_x) descend xs n
One x ->
if n < size_x then sel x n else
select (2*size_x) descend xs (n-size_x)
where
descend (l,r) m | m < size_x = sel l m
| otherwise = sel r (m-size_x)Since the sub tree, which we expect in descend is exactly twice as large as x, in other words a pair of one nesting more, the size of x exactly fits to the parameter of function sel. In the descend function we add another pair nesting and can reuse the function sel for the left resp. right subtree.
We define modify in the same way. Instead of a generalized selection function we now have a generalized modify function. This however is simplre, because the values are never passed from one level of nesting to another one. Therefore, we can avoid introducing another type varibale, which generalizes the deaper nesting of pairs.
modify :: Int -> (a -> a) -> ArrayList a -> ArrayList a
modify _ _ Empty =
error "ArrayList.modify: empty list"
modify n f (NonEmpty l) =
NonEmpty $ update 1 upd n l
where
upd m x
| m == 0 = f x
| otherwise =
error $ "ArrayList.modify: invalid index "
++ show n
update :: Int
-> (Int -> a -> a)
-> Int -> TreeList a -> TreeList a
update _ upd n (Single x) = Single $ upd n xLike in select we change the update function within the recursion and construct a new update function, which applies the passed update function to the correct sub tree.
update size_x upd n (bit :< xs) =
case bit of
Zero ->
Zero :< update (2*size_x) descend n xs
One x ->
if n < size_x then One (upd n x) :< xs else
bit :<
update (2*size_x) descend (n-size_x) xs
where
descend m (l,r)
| m < size_x = (upd m l, r)
| otherwise = (l, upd (m-size_x) r)This completes the implementation of type-safe array lists. We no longer need to use QuickCheck to test whether the invariants hold, since this is already ensured by the type check. We should of course still write tests that check the correctness of the operations. There can still be bugs, for instance one could select the wrong subtree, when descending with the helper select od update function.
In the chapter about array we saw that we can efficiently map indexes of type Int or Integer to values. In this chapter we will discuss data structures, so-called Tries [^ trie], which generalzies the idea of arrays to arbitrary key types, other than numbers.
The idea behind tries is different from a direct representation of the keys within a search tree or a (sorted) list of key-value pairs. We start with a trie structure, where keys are strings. Here a trie is a tree where each edge is labelled with a letter. Then the represented keys are the strings which can be read along a path from the root to a node within the trie. If this string is a valid key within the trie, we store the corrsponding value within this node, otherwise the node is empty. As an example, we consider the following mapping:
"to" -> 17
"tom" -> 42
"tea" -> 11
"ten" -> 10Which results into the following trie:
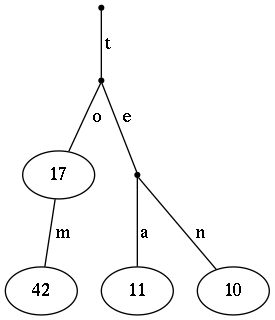
String-Trie
Note, that there is no information stored for the words "t" and "te". Furthermore, we stored the number 17 within the node related to the word "to", althoug this node is not a leaf an we can descend further to the word "tom".
Althoug one might have the impression, that a trie could branch unrestrictedly, this is not the case, because the alphabet is restricted and branching is only possible up to the degree 26 or perhaps 256 considering ASCII code.
In the implementation we start with an implementation for mappings from characters to values. A very simple (although perhaps not most efficient) implementation could be
type CharMap a = [(Char,a)]The empty map is represented by the empty list.
emptyCharMap :: CharMap a
emptyCharMap = []Also looking up a character is simple:
lookupChar :: Char -> CharMap a -> Maybe a
lookupChar _ [] = Nothing
lookupChar c ((c',x):xs)
| c == c' = Just x
| otherwise = lookupChar c xsInserting a new entry is possible, by putting it in front of the list and deleting a possible existing other accurece of the same key:
insertChar :: Char -> a -> CharMap a -> CharMap a
insertChar c x xs = (c,x) : deleteChar c xsDeleting an entry can be implemented by filter:
deleteChar :: Char -> CharMap a -> CharMap a
deleteChar c = filter ((c/=) . fst)An implemtation using a balanced search tree or an Data.IntMap over the ASCII values would be more efficient and should be used in practice. However, since the length of the list here ist restricted to a finite set of characters, the difference between these implementation is only a constant factor nd not relevant for the run time complexity of the algorithms.
As a next step we can resuse the CharMap to define a data structure for string tries as follows:
data StringMap a =
StringMap (Maybe a) (CharMap (StringMap a))The CharMap is used to store the edge lables of the trie. For the example from above, we obtain:
StringMap Nothing
[('t',StringMap Nothing
[('o',StringMap (Just 17)
[('m',StringMap (Just 42) [])])
,('e',StringMap Nothing
[('a',StringMap (Just 11) [])
,('n',StringMap (Just 10) [])])])]The empty StringMap is only the root (representing the empty word) without a corresponding entry.
emptyStringMap :: StringMap a
emptyStringMap = StringMap Nothing emptyCharMapFor looking up a String we successively descend through the nested maps:
lookupString :: String -> StringMap a -> Maybe aIf the key is the empty String, we return the local Maybe value.
lookupString [] (StringMap a _) = aOtherwise, we descend through the CharMap and further through the corresponding StringMap. Using the Maybe monad is useful here:
lookupString (c:cs) (StringMap _ b) =
lookupChar c b >>= lookupString csTo insert a value with respect to a given String, we have to walk along the path if it already exists or have to add the path in the other case.
insertString :: String -> a -> StringMap a -> StringMap a
insertString [] x (StringMap _ b) = StringMap (Just x) b
insertString (c:cs) x (StringMap a b) = StringMap a $
case lookupChar c b of
Nothing ->
insertChar c
(insertString cs x emptyStringMap) b
Just m ->
insertChar c
(insertString cs x m) bThis is simple for the empty string. In the case for a non-empty string we have to use lookupChar to obtain the tree in which we should descend. If this tree does not exist (Nothing case), we have to construct it (emptyStringMap).
In both cases, we have to use insertChar c and insertString cs in the same way. Hence, we can push the branching into these calls and implement it by means of the predefined function maybe :: b -> (a -> b) -> Maybe a -> b:
insertString (c:cs) x (StringMap a b) =
StringMap a
(insertChar c
(insertString cs x
(maybe emptyStringMap id (lookupChar c b)))
b)The runtime of insertString is linear ith respect to the length of the key. This is different from the runtime for balanced search trees, where the runtime is linear in the length of the key and logarithmic in the number of stored values.
Deleting an element works similar:
deleteString :: String -> StringMap a -> StringMap aIf the key is empty we can delet it localy:
deleteString [] (StringMap _ b) =
StringMap Nothing bOtherwise we lookup the first cahracted in the CharMap. If this does not exist, we are done, otherwise we recursively delete the substructures.
deleteString (c:cs) (StringMap a b) =
case lookupChar c b of
Nothing -> StringMap a b
Just m ->
StringMap a
(insertChar c (deleteString cs d) b)Again we can combine both cases, which however is less efficient for the case that the value did not occure at all.
deleteString (c:cs) (StringMap a b) =
StringMap a
(maybe b
(\d -> insertChar c (deleteString cs m) b)
(lookupChar c b))in contrast to the type of an purely (without nested) polymorphic, rekursive function↩