Ausgewählte Programmiertechniken

Dieses Kapitel behandelt funktionale Programmiertechniken, die häufig eingesetzt werden, um Programme effizienter zu machen.

Differenzlisten

Zu Beginn der Vorlesung haben wir unterschiedliche Implementierungen der reverse-Funktion kennen gelernt. Eine naive Implementierung mit quadratischer Laufzeit:

reverse :: [a] -> [a]
reverse []     = []
reverse (x:xs) = reverse xs ++ [x]

und eine Implementierung mit linearer Laufzeit, die die Akkumulatortechnik verwendet:

reverse :: [a] -> [a]
reverse l = rev l []
 where
  rev []     ys = ys
  rev (x:xs) ys = rev xs (x:ys)

Hierbei ist rev :: [a] -> [a] -> [a].

Wir wollen nun versuchen, die Klarheit der ersten Implementierung mit der Effizienz der zweiten zu vereinen. Die erste Implementierung ist schneller verständlich als die zweite, da sie einem einfacheren Rekursions-Schema folgt. Die zweite Implementierung ist komplizierter, da sich hier zwei Argumente der rekursiven Funktion im rekursiven Aufruf auf trickreiche Weise ändern.

Dank Currying ist rev auch eine einstellige Funktion, nämlich vom Typ [a] -> ([a] -> [a]). Wir schreiben sie nun so um, dass dies auch in ihrer Implementierung sichtbar wird.

reverse :: [a] -> [a]
reverse l = rev l []
 where
  rev []     = id
  rev (x:xs) = rev xs . (x:)

Die rev-Funktion hat nun dieselbe rekursive Struktur wie die naive Implementierung von reverse. id spielt dabei die Rolle der leeren Liste, (.) die Rolle der Konkatenation mit (++) und (x:) repräsentiert die einelementige Liste [x]. Wir haben also nur das Listen-Monoid durch das Funktions-Monoid ersetzt und dadurch die Effizienz der reverse-Funktion verbessert.

Wir können diese Idee in einem abstrakten Datentyp sogenannter Differenzlisten¹ ausdrücken. Ein weiterer verwendeter Name dieser Datenstruktur ist Funktionale Liste, da die Liste als Funktion dargestellt wird.

import Data.Monoid

newtype DList a = DList ([a] -> [a])

instance Monoid (DList a) where
  mempty                      = DList id
  DList xs `mappend` DList ys = DList (xs . ys)

Die Implementierung von mappend ist nicht rekursiv und hat daher konstante Laufzeit, was im Kern der Grund für die Laufzeitverbesserung ist.

Wie in der letzten Implementierung von reverse können wir eine Differenzliste in eine normale Liste umwandeln, indem wir sie auf die leere Liste anwenden.

fromDList :: DList a -> [a]
fromDList (DList xs) = xs []

Intuitiv ist eine Differenzliste eine Funktion, die die in ihr enthaltenen Elemente vorne an ihr Argument anhängt. Eine normale Liste kann also wie folgt in eine Diffrenzliste konvertiert werden.

toDList :: [a] -> DList a
toDList xs = DList (xs ++)

Wir können die Implementierung der reverse-Funktion umschreiben, um deutlich zu machen, dass wir Differenzlisten verwenden.

reverse :: [a] -> [a]
reverse l = fromDList (rev l)
 where
  rev []     = mempty
  rev (x:xs) = rev xs `mappend` toDList [x]

Diese Implementierung verwendet die (++)-Funktion nur durch toDList und nur mit einelementigen Listen als erstem Argument. Sie hat daher wie die Implementierung mit Akkumulatortechnik lineare Laufzeit.

Differenzlisten werden typischerweise bei Baumdurchläufen verwendet, die eine Liste erzeugen. Als Beispiel betrachten wir einen Baumdurchlauf, bei dem wir die Knotenbeschriftungen in Infix-Ordnung auflisten. Die naive Implementierung verwendeten das Ergebnis des rekursiven Aufrufs als linkes Argument von (++) und wir habe im schlechtesten (unbalancierten) Fall eine quadratische Laufzeit.

Mit Differenzlisten können wir die Beschriftungen in Linearzeit auflisten:

data Tree a = Empty
            | Node (Tree a) a (Tree a)
 deriving Eq

infixLabels :: Tree a -> [a]
infixLabels = fromDList . labels
 where
  labels Empty          = mempty
  labels (Branch l x r) =
    labels l `mappend` toDList [x]
             `mappend` labels r

Die Funktionen toDList und fromDList sind zueinander inverse Monoid-Isomorphismen (einfacher Induktionsbeweis). Man kann daher jedes Programm über Listen, das nur die Monoid-Operationen verwendet, in eines über Differenzlisten umschreiben, ohne dessen Verhalten zu ändern.

Nicht jede Funktion, die man auf Listen schreiben kann, kann man auch direkt auf Differenzlisten implementieren. Zum Beispiel können wir nicht testen, ob eine Differenzliste leer ist, ohne sie in eine normale Liste zu konvertieren:

nullDL :: DList a -> Bool
nullDL (DList dl) = null (dl [])

Das einzige, was wir mit der Funktion dl machen können, ist sie anzuwenden. Anders können wir nicht sehen, wie viele Elemente sie vor ihr Argument hängt. Dieses Problem könnte man noch umgehen, indem man zusätzlich eine Zahl für die Länge der Liste speichert (welche es gleichzeitig erlauben würde, eine length-Funktion zu definieren). Dieser Trick hat aber seine Grenzen. Auch er erlaubt es nicht Funktionen, wie map- oder concat auf Differenzlisten zu implementieren, wie der folgende Versuch zeigt:

mapDL :: (a -> b) -> DList a -> DList b
mapDL f (DList dl) = DList (\l -> ???)

Wir können die Funktion f nicht auf die Elemente von dl anwenden, ohne dl in eine normale Liste zu konvertieren. Ähnliche Probleme haben wir bei der Implementierung einer concat-Funktion.

Wir werden später eine andere Implementierung von Listen als Funktionen kennen lernen, die die Definition von map und concat erlaubt.

Ein anderes typisches Beispiel für Baumdurchläufe, die Listen erzeugen, sind show-Funktionen. Die Show-Klasse enthält folgende Funktionen²:

class Show a where
  show :: a -> String
  show x = shows x ""

  showsPrec :: Int -> a -> ShowS

Der ShowS-Typ und die shows-Funktion sind dabei wie folgt definiert:

type ShowS = String -> String

shows :: Show a => a -> ShowS
shows = showsPrec 0

Der ShowS-Typ repräsentiert also Strings als Differenzlisten und shows verhält sich wie die show-Funktion, verwendet aber Differenzlisten. Die Funktion showsPrec bekommt einen zusätzlichen Parameter, den man verwenden kann, um unter Berücksichtigung von Präzedenzen Klammern zu sparen. Wir werden ihn im Folgenden aber ignorieren.

Mit Hilfe des ShowS-Typen können wir Bäume in Linearzeit in Strings umwandeln.

instance Show a => Show (Tree a) where
  showsPrec _ Empty =
    showString "Empty"
  showsPrec _ (Branch l x r) =
    showString "Branch " .
    showParen (l/=Empty) (shows l) .
    showChar ' ' . shows x . showChar ' ' .
    showParen (r/=Empty) (shows r)

Analog zum DList-Typ verwenden wir Funktionskomposition statt Listenkonkatenation um lineare Laufzeit zu erreichen.

Die Funktion showString entspricht der Funktion toDList und erzeugt aus einem String einen ShowS-Wert.

showString :: String -> ShowS
showString = (++)

showChar tut das selbe für ein einzelnes Zeichen:

showChar :: Char -> ShowS
showChar = (:)

showParen erzeugt Klammern um einen ShowS-Wert, falls das übergebene Flag True ist.

showParen :: Bool -> ShowS -> ShowS
showParen True  s = showChar '(' . s . showChar ')'
showParen False s = s

All diese Funktionen sind in der Prelude definiert.

Continuations

Als Beispiel für die Maybe-Monade haben wir einen Datentyp

data Expr = Num Float
          | Expr :+: Expr
          | Expr :/: Expr

und eine Funktion

eval :: Expr -> Maybe Float

definiert, wobei die eval-Funktion Nothing liefert, wenn bei der Auswertung eine Division durch Null auftritt.

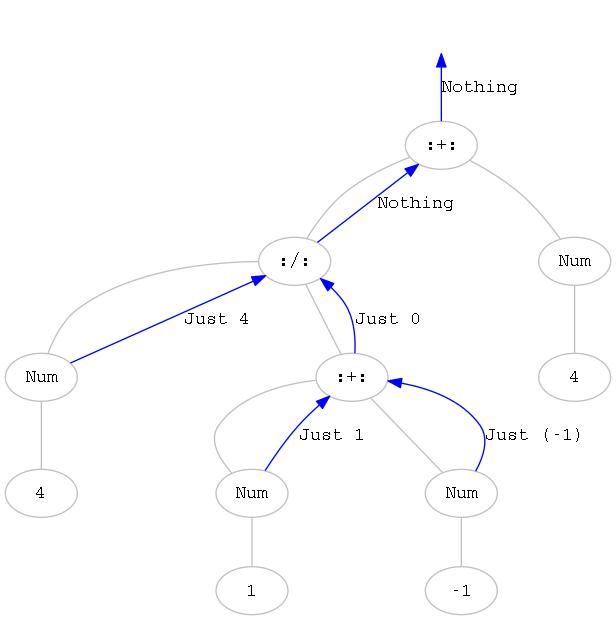
Das folgende Bild stellt den Baumdurchlauf für die Auswertung des Ausdrucks

Num 4 :/: (Num 1 :+: Num (-1)) :+: Num 4

grafisch dar.

Bild von einem Baumdurchlauf

Sobald der Wert Nothing auftritt, wird der Baumdurchlauf abgebrochen. Zum Beispiel wird das rechte Argument des obersten :+:-Knotens nicht mehr ausgewertet, da die Auswertung des linken Arguments fehlschlägt.

Der Wert Nothing wird von der Stelle im Baum, an der er zuerst auftritt, bis zur Wurzel des Ausdrucks hoch gereicht. Die eval-Funktion testet dazu, ob die Ergebnisse von rekursiven Aufrufen Nothing sind und gibt in diesem Fall selbst Nothing zurück. Wenn ein Nothing-Wert sehr tief im Baum auftritt, ist dieses Hochreichen ineffizient. Können wir die Abarbeitung nicht stoppen, ohne den Fehler durch den Baum zu reichen?

Um dies zu erreichen, schreiben wir die eval-Funktion in Continuation Passing Style (CPS). Eine Funktion in CPS nimmt als zusätzliches Argument eine Funktion, die sogenannte Continuation, welche die weitere Berechnung repräsentiert. In CPS hat die eval-Funktion den folgenden Typ:

evalCPS :: Expr
        -> (Float -> Maybe Float)
        -> Maybe Float

Der Continuation übergeben wir das Ergebnis, das wir im Erfolgsfall zurück liefern würden. Die Regel für Konstanten sieht deshalb so aus:

evalCPS (Num x) k = k x

Um mehrere Ausdrücke hintereinander auszuwerten, schachteln wir die zweite Auswertung in der Continuation der ersten:

evalCPS (e1 :+: e2) k =
  evalCPS e1 (\v1 -> evalCPS e2 (\v2 -> k (v1 + v2)))

Die übergebene Continuation wird ganz innen benutzt. Im Fehlerfall geben wir als Ergebnis der Continuation Nothing zurück statt die übergebene Continuation aufzurufen:

evalCPS (e1 :/: e2) k =
  evalCPS e1 (\v1 ->
   evalCPS e2 (\v2 ->
    if v2 == 0 then Nothing else k (v1 / v2)))

In diesem Program gibt es kein Pattern-Matching auf Nothing mehr! Im Fehlerfall gibt evalCPS direkt Nothing zurück, ohne es durch den Berechnungsbaum hindurch zu reichen.

Eine alternative Implementierung der letzten Regel berechnet den Divisor zuerst und spart die Berechnung des Dividenden, wenn der Divisor Null ist:

evalCPS (e1 :/: e2) k =
  evalCPS e2 (\v2 ->
   if v2 == 0 then Nothing
    else evalCPS e1 (\v1 -> k (v1 / v2)))

Rufen wir evalCPS mit dem obigen Ausdruck auf, können wir Just als Continuation übergeben um ein Ergebnis vom Typ Maybe Float zu erhalten.

    ghci> let zero = Num 1 :+: Num (-1)
    ghci> let expr = (Num 4 :/: zero) :+: Num 4
    ghci> evalCPS expr Just
    Nothing

Wir werten diesen Aufruf schrittweise aus:

      evalCPS expr Just
    = evalCPS ((Num 4 :/: zero) :+: Num 4) Just
    = evalCPS (Num 4 :/: zero) (\x ->
       evalCPS (Num 4) (\y -> Just (x+y)))
    = evalCPS zero (\b ->
       if b==0 then Nothing
        else evalCPS (Num 4) (\a ->
         evalCPS (Num 4) (\y -> Just ((a/b)+y))))
    = evalCPS (Num 1 :+: Num (-1)) (\b ->
       if b==0 then Nothing
        else evalCPS (Num 4) (\a ->
         evalCPS (Num 4) (\y -> Just ((a/b)+y))))
    = evalCPS (Num 1) (\c ->
       evalCPS (Num (-1)) (\d ->
        if (c+d)==0 then Nothing
         else evalCPS (Num 4) (\a ->
          evalCPS (Num 4) (\y ->
           Just ((a/(c+d))+y)))))
    = evalCPS (Num (-1)) (\d ->
       if (1+d)==0 then Nothing
        else evalCPS (Num 4) (\a ->
         evalCPS (Num 4) (\y ->
          Just ((a/(1+d))+y))))
    = if (1+(-1))==0 then Nothing
       else evalCPS (Num 4) (\a ->
        evalCPS (Num 4) (\y ->
         Just ((a/(1+d))+y)))
    = Nothing

Der Wert Nothing wird also sofort zurück gegeben, wenn er auftritt und nicht mehr durch den Aufrufbaum gereicht.

Die hier gezeigte Funktion evalCPS ist zwar effizienter als die Funktion eval in der Maybe-Monade aber auch weniger gut lesbar. Wir werden nun sehen, dass die neue Implementierung auch monadisch ist, nämlich bezüglich einer Continuation-basierten Variante der Maybe-Monade.

Inspiriert vom Typ von evalCPS definieren wir den folgenden Datentyp:

newtype CMaybe r a = CMaybe ((a -> Maybe r) -> Maybe r)

Dieser Typ entspricht dem Ergebnistyp von evalCPS, wobei Float durch die Typparameter r und a ersetzt wurde. Werte von CMaybe kann man in normale Maybe-Werte konvertieren, indem man Just als Continuation übergibt:

fromCMaybe :: CMaybe a a -> Maybe a
fromCMaybe (CMaybe ca) = ca Just

Beim Konvertieren eines CMaybe-Wertes werden die Typparameter r und a unifiziert. Vor der Konvertierung bleibt r in der Regel polymorph.

Wir definieren nun eine Monad-Instanz für CMaybe r mit deren Hilfe man CMaybe-Werte definieren kann.

instance Monad (CMaybe r) where
  return x = CMaybe (\k -> k x)

  CMaybe ca >>= f = CMaybe (\k ->
    ca (\x -> let CMaybe cb = f x in cb k))

Die Implementierung von return übergibt das Argument an die Continuation und die Implementierung von >>= schachtelt die Berechnung des zweiten Arguments in der Continuation des ersten. Dadurch ist das Ergebnis der Continuation vom Typ Maybe b das Argument aber vom Typ a. Anders als bei der Maybe-Monade ist >>= ohne Pattern-Matching definiert.

Die Monadengesetze zeigen wir unabhängig vom Ergebnistyp der Continuation. Wir ignorieren dabei der Übersichtlichkeit wegen die newtype-Konstruktoren:

      return x >>= f
    = (\k -> k x) >>= f
    = (\k' -> (\k -> k x) (\x' -> f x' k'))
    = (\k' -> (\x' -> f x' k') x)
    = (\k' -> f x k')
    = f x

      ca >>= return
    = (\k -> ca (\x -> return x k))
    = (\k -> ca (\x -> (\k' -> k' x) k))
    = (\k -> ca (\x -> k x))
    = (\k -> ca k)
    = ca

      (ca >>= f) >>= g
    = (\k -> ca (\x -> f x k)) >>= g
    = \k' -> (\k -> ca (\x -> f x k))
              (\y -> g y k')
    = \k' -> ca (\x -> f x (\y -> g y k'))
    = \k' -> ca (\x -> (\k ->
                 f x (\y -> g y k)) k')
    = \k' -> ca (\x -> (f x >>= g) k')
    = ca >>= \x -> f x >>= g

Sowohl die Implementierung der Monadenoperationen als auch die Beweise für die Monadengesetze sind unabhängig vom Ergebnistyp Maybe r der Continuation. Wir werden später weitere Continuation-Monaden kennen lernen, für die die Definition der Monadenoperationen (also auch die Beweise der Gesetze) mit den oben gezeigten übereinstimmen.

Wir geben nun eine MonadPlus-Instanz für CMaybe an, die die entsprechenden Operationen des Maybe-Typs liftet.

instance MonadPlus (CMaybe r) where
  mzero = CMaybe (\_ -> mzero)

  CMaybe ca `mplus` CMaybe cb =
    CMaybe (\cont -> ca cont `mplus` cb cont)

Auch für diese Instanz zeigen wir die Gesetze unter Vernachlässigung der newtype-Konstruktoren.

      mzero >>= f
    = (\_ -> mzero) >>= f
      \k -> (\_ -> mzero) (\x -> f x k)
    = \k -> mzero
    = mzero

      (ca `mplus` cb) >>= f
    = \k -> (ca `mplus` cb) (\x -> f x k)
    = \k -> (\k' -> ca k' `mplus` cb k')
             (\x -> f x k)
    = \k -> ca (\x -> f x k)
             `mplus` cb (\x -> f x k)
    = \k -> (\k' -> ca (\x -> f x k')) k
             `mplus` (\d -> cb (\x -> f x k')) k
    = (\k' -> ca (\x -> f x k'))
       `mplus` (\k' -> cb (\x -> f x k'))
    = (ca >>= f) `mplus` (cb >>= f)

Die CMaybe-Monade erfüllt also, anders als die Maybe-Monade, das Distributivgesetz zwischen >>= und mplus und kann daher zur Implementierung von Backtracking verwendet werden.

    ghci> let a = return False `mplus` return True
    ghci> let b = a >>= guard
    ghci> b :: Maybe ()
    Nothing
    ghci> fromCMaybe b
    Just ()

Wir können nun die monadische Implementierung der eval-Funktion

eval :: MonadPlus m => Expr -> m Float
eval (Num x) = return x
eval (a :+: b) =
  do x <- eval a
     y <- eval b
     return (x+y)
eval (a :/: b) =
  do y <- eval b
     guard (y/=0)
     x <- eval a
     return (x/y)

in der CMaybe-Monade ausführen, was einer Ausführung mit der evalCPS-Funktion entspricht.

Die Maybe-Monade ist nicht die einzige, die man mit Continuations kombinieren kann. Wenn wir im CMaybe-Typ Maybe durch DList ersetzen, erhalten wir eine Continuation-basierte Listenmonade.

Wir haben gesehen, dass die obige Implementung von mplus der CMaybe-Monade das Gesetz

    (a `mplus` b) >>= f  =  (a>>=f) `mplus` (b>>=f)

erfüllt, obwohl die mplus-Funktion der Maybe-Monade es nicht erfüllt. Diese erfüllt stattdessen das Gesetz

    return x `mplus` a  =  return x

das an ein Gesetz für catch in Fehlermonaden erinnert: Nur wenn das linke Argument fehlschlägt wird das rechte Argument ausgeführt.

Können wir eine Funktion orElse für die CMaybe-Monade definieren, die das Gesetz

    return x `orElse` a  =  return x

erfüllt? Das können wir:

orElse :: CMaybe a a -> CMaybe a a -> CMaybe r a
CMaybe ca `orElse` CMaybe cb =
  CMaybe (\k -> (ca Just `mplus` cb Just) >>= k)

Diese Implementierung übergibt Just als Continuation an beide Alternativen, ruft auf den Ergebnissen die mplus-Funktion der Maybe-Monade auf und übergibt das Ergebnis dieses Aufruf mit dem bind-Operator der Maybe-Monade an die Continuation k. Im Typ von orElse ist der Typ-Parameter r der Argumente gleich a, da wir wie in fromCMaybe die Continuation Just :: a -> Maybe a übergeben.

Wenn wir die mplus-Funktion der Maybe-Monade auf diese Weise in den CMaybe-Typ heben, überträgt sich die obige Eigenschaft:

      return x `orElse` a
    = (\k -> ((return x) Just `mplus` a Just)
              >>= k)
    = (\k -> ((\k' -> k' x) Just `mplus` a Just)
              >>= k)
    = (\k -> (Just x `mplus` a Just) >>= k)
    = (\k -> Just x >>= k)
    = (\k -> k x)
    = return x

orElse verhält sich also genauso wie mplus in der Maybe-Monade:

    ghci> let a = return False `orElse` return True
    ghci> fromCMaybe (a >>= guard)
    Nothing

Diese Methode, einen Wert aus der unterliegenden Maybe-Monade mit dem bind-Operator an die Continuation zu übergeben, kann man anwenden um beliebige Werte vom Maybe-Typ in den CMaybe-Typ zu heben:

toCMaybe :: Maybe a -> CMaybe r a
toCMaybe a = CMaybe (\k -> a >>= k)

Die Funktion toCMaybe ist dabei ein Monaden-Homomorphismus, das heißt es gilt:

    toCMaybe (return x)  =  return x
    toCMaybe (a >>= f)   =  toCMaybe a >>= toCMaybe . f

Hier die Beweise:

      toCMaybe (return x)
    = \k -> return x >>= k
    = \k -> k x
    = return x

      toCMaybe (a >>= f)
    = \k -> (a >>= f) >>= k
    = \k -> a >>= (\w -> f w >>= k)
    = \k -> (\k3 -> a (\u -> (f u >>= k) k3))
    = \k -> (\k3 -> a (\u -> (\k5 ->
        f u (\v -> k v k5)) k3))
    = \k -> (\k3 -> a (\u -> f u (\v -> k v k3)))
    = \k -> (\k1 -> (\k3 -> a (\u -> k1 u k3)))
       (\y -> (\k4 -> f y (\v -> k v k4)))
    = \k -> (\k1 -> (\k3 -> a (\u -> k1 u k3)))
       (\y -> (\k2 -> \k4 ->
        f y (\v -> k2 v k4)) k)
    = (\k1 -> (\k3 -> a (\u -> k1 u k3)))
       >>= \z -> \k2 -> \k4 -> f z (\v -> k2 v k4)
    = (\k1 -> a >>= k1) >>= \z -> \k2 -> f z >>= k2
    = toCMaybe a >>= toCMaybe . f

In den Beweisen verwenden wir die Links-Identität sowie das Assoziativgesetz der unterliegenden Maybe-Monade.

Continuation-basierte Listen

Bei den Instanzen für den CMaybe-Typ haben wir (im Gegensatz zur Definition von orElse) nicht ausgenutzt, dass Maybe eine Monade ist. Die Monad-Instanz verwendet gar keine Operationen des unterliegenden Typs, die MonadPlus-Instanz nur die Monoid(-artigen) Operationen mzero und mplus.

Wir können also die selbe Konstruktion für andere Monoide durchführen und wählen als Beispiel Differenzlisten:

newtype CList r a =
  CList ((a -> DList r) -> DList r)

Solche Continuation-Listen können wir in normale Listen konvertieren, indem wir zuerst (:) als Continuation übergeben und dann der Differenzliste die leere Liste übergeben:

fromCList :: CList a a -> [a]
fromCList (CList ca) =
  fromDList (ca (DList . (:)))

Analog zur MonadPlus-Instanz für CMaybe r können wir eine Monoid-Instanz für CList r a definieren:

instance Monoid (CList r a) where
  mempty = CList (\_ -> mempty)

  CList ca `mappend` CList cb =
    CList (\k -> ca k `mappend` cb k)

Die Monad-Instanz für CList r definieren wir genau wie die für CMaybe r:

instance Monad (CList r) where
  return x = CList ($x)
  CList ca >>= f =
   CList (\k -> ca (\x -> let CList cb = f x
                           in cb k))

Die Monaden-Gesetze brauchen wir nicht zu beweisen, da die Beweise für CMaybe r vom Ergebnistyp der Continuation unabhängig sind und daher auch für CList gelten.

Da DList keine Monade ist können wir Differenzlisten nicht analog zu Maybe-Werten in den CList-Typ heben (dazu bräuchten wir >>=). Stattdessen können wir ausnutzen, dass sowohl Listen als auch Continuation-Listen Monoide sind und einen Monoid-Isomorphismus definieren:

toCList :: [a] -> CList r a
toCList = foldr mappend mempty . map return

Continuation-Listen können mehr als Differenzlisten, da sie Instanz der Monad-Klasse sind. Das können wir ausnutzen, um zum Beipsiel eine map- und eine concat-Funktion zu definieren:

mapCL :: (a -> b) -> CList r a -> CList r b
mapCL f cl = cl >>= return . f

concatCL :: CList r (CList r a) -> CList r a
concatCL cl = cl >>= id

Allerdings ist es noch immer nicht möglich einen Leerheitstest oder eine length-Funktion zu definieren, ohne eine Continuation-Liste in eine normale Liste zu konvertieren.

Um dieses Manko auszumerzen, definieren wir eine weitere Variante des Continuation-Typs, die kein spezielles Monoid mehr verwendet.

newtype C m a = C ((a -> m) -> m)

Der Ergebnistyp ist jetzt polymorph vom Typ m. Um eine Monoid-Instanz zu definieren, fordern wir nun, dass m ein Monoid ist.

instance Monoid m => Monoid (C m a) where
  mempty              = C (\_ -> mempty)
  C ca `mappend` C cb = C (\k -> ca k `mappend` cb k)

Die Monad-Instanz sieht aus wie immer.

instance Monad (C m) where
  return x   = C ($x)
  C ca >>= f = C (\k -> ca (\x -> let C cb = f x in cb k))

Um einen Wert vom Typ C m a nach m zu konvertieren übergeben wir eine Continuation vom Typ (a -> m).

fromC :: Monoid m => (a -> m) -> C m a -> m
fromC f (C ca) = ca f

Als Konvertierung in die andere Richtung definieren wir wieder einen Monoid-Homomorphismus von Listen in C m a:

toC :: Monoid m => [a] -> C m a
toC = foldr mappend mempty . map return

Nun können wir einen Leerheitstest als Monoid-Homomorphismus von C m a in (Bool,&&,True) definieren, das heißt als Funktion nullC mit den Eigenschaften:

    nullC mempty           =  True
    nullC (a `mappend` b)  =  nullC a && nullC b

Dieses boolesche Monoid ist in Haskell in Data.Monoid wie folgt vordefiniert:

newtype All = All { getAll :: Bool }

instance Monoid All where
  mempty = All True

  x `mappend` y = All (getAll x && getAll y)

Analog dazu gibt es einen newtype Any, der das Monoid (Bool,||,False) repräsentiert.

Monoid-Homomorphismen von C m a in m definiert man, indem man als Continuation eine Funktion f :: a -> m übergibt. Das jede sich so ergebende Funktion ein Homomorphismus ist, folgt direkt aus der Definition der Monoid-Instanz für C m a:

      fromC f mempty
    = fromC f (\_ -> mempty)
    = (\_ -> mempty) f
    = mempty

      fromC f (a `mappend` b)
    = fromC f (\k -> a k `mappend` b k)
    = a f `mappend` b f
    = fromC f a `mappend` fromC f b

Zusätzlich zu den Homomorphie-Gesetzen erfüllen solche Funktionen die Eigenschaft:

    fromC f (return x)  =  f x

Denn:

      fromC f (return x)
    = return x f
    = (\k -> k x) f
    = f x

Die Funktion nullC definieren wir also als Homomorphismus, der jedem Listenelement den Wert False zuordnet.

nullC :: C All a -> Bool
nullC l = getAll (fromC (\_ -> All False) l)

Analog dazu können wir eine lengthC-Funktion als Homomorphismus in (Int,+,0) definieren:

lengthC :: C (Sum Int) a -> Int
lengthC l = getSum (fromC (\_ -> Sum 1) l)

Hierbei ist Sum Int ein newtype um Int, der das Monoid (Int,+,0) darstellt. Analog dazu gibt es Prod für das Monoid (Int,*,1).

Wir können nun die Länge einer Continuation-Liste mit Hilfe der Gesetze wie folgt berechnen:

      lengthC (return 1 `mappend` return 2)
    = lengthC (return 1) + lengthC (return 2)
    = 1 + 1
    = 2

Als Kontrolle berechnen wir es auch einmal anhand der Definitionen der beteiligten Funktionen.

      lengthC (return 1 `mappend` return 2)
    = fromC (\_ -> 1) (return 1 `mappend` return 2)
    = (return 1 `mappend` return 2) (\_ -> 1)
    = (\k -> return 1 k + return 2 k) (\_ -> 1)
    = return 1 (\_ -> 1) + return 2 (\_ -> 1)
    = (\k -> k 1) (\_ -> 1) + (\k -> k 2) (\_ -> 1)
    = 1 + 1
    = 2

Unsere Implementierung hat noch einen entscheidenden Nachteil: Der Ergebnistyp m der Continuation, ist nach außen sichtbar und kann deshalb nicht gleichzeitig mit unterschiedlichen Typen instanziiert werden. Zum Beispiel können wir keine Funktion schreiben, die gleichzeitig testet ob eine Liste leer ist und ihre Länge berechnet. Die folgende Definition führt zu einem Typfehler.

nullLength l = (nullC l, lengthC l)

Hier müsste der Parameter m sowohl mit All als auch mit Sum Int belegt werden:

Couldn't match expected type `Sum Int'
against inferred type `All'

Alle durch die Monoid oder Monaden-Instanzen erzeugten Listen haben einen polymorphen Typ m, das sieht man der Definition des Typs aber nicht an.

Mit einer Typsystem-Erweiterung, sogenannten Polymorphen Typen höheren Rangs, können wir der obige Funktion aber einen korrekten Typ geben. Mit der Spracherweiterung RankNTypes können wir die Typen der beteiligten Funktionen wie folgt anpassen:

nullC      :: (forall m . Monoid m => C m a) -> Bool
lengthC    :: (forall m . Monoid m => C m a) -> Int
nullLength :: (forall m . Monoid m => C m a) -> (Bool, Int)

Die Definitionen der Funktionen bleiben unverändert.

Solche Typen können nicht inferiert werden und explizit polymorphe Argumente kann man auch nicht per Currying weglassen. Hätten wir das Argument l bei einer der drei Funktionen nicht explizit hingeschrieben oder eine Typsignatur weggelassen, hätte der GHC einen Typfehler ausgegeben.

Solche Typsignaturen sind sehr umständlich. Besser ist es, die Typvariable m gar nicht erst nach außen sichtbar zu machen, indem man sie schon bei der Typ-Deklaration als polymorph deklariert:

newtype List a = List (forall m . Monoid m => (a -> m) -> m)

Alle Definitionen für C m lassen sich auf List übertragen. Die Typsignaturen werden dabei dadurch vereinfacht, dass List nur noch einen Typ-Parameter a hat.