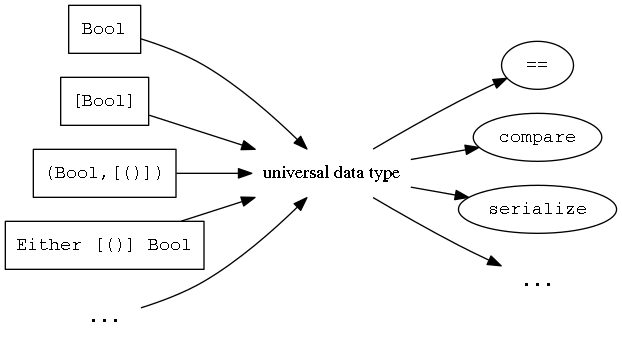
Avoiding quadratic number of function definitions with universal datatype
Der Begriff Generische Programmierung wird für verschiedene Konzepte verwendet. Zum Beispiel nennt man das, was in Java Generics heißt, in Haskell Polymorphie, aber auch das Konzept der Überladung, zum Beispiel arithmetischer Funktionen, wird gelegentlich als generisch bezeichnet. In diesem Kapitel behandeln wir sogenannte Datentyp-generische Programmierung, mit deren Hilfe man gleichartige Funktionen auf unterschiedlichen Datentypen mit Hilfe einer einzigen Implementierung definieren kann.
Im vorigen Kapitel haben wir Tries für unterschiedliche Datenstrukturen kennengelernt und dabei gesehen, dass Implementierungen sowohl der Map-Typen als auch der zugehörigen Funktionen einem festen Schema folgen. Bereits früher sind wir solchen Funktionen begegnet, die zwar für unterschiedliche Datentypen gleichartig, aber nicht identisch, implementiert werden.
Zum Beispiel folgt der Gleichheits-Test in der Regel einem festen Muster. Trotzdem kann man keine allgemeine Implementierung für
(==) :: a -> a -> Boolangeben, da sich die Implementierungen für unterschiedliche Typen unterscheiden. In Haskell wurde deshalb die Typklasse Eq eingeführt, die es erlaubt, für unterschiedliche Datentypen unterschiedliche Implementierungen für == anzugeben. Da solche Implementierungen sich in der Regel ähneln, gibt es außerdem die Möglichkeit, Eq-Instanzen automatisch vom Compiler nach einem festen Muster generieren zu lassen (Schlüsselwort deriving). Eine Alternative zu solch speziellem Compiler-Support ist die im Folgenden vorgestellte Datentyp-generische Programmierung.
Statt ein festes Muster zur Implementierung von == für unterschiedliche Datentypen immer wieder anzuwenden, kann man es ein einziges Mal für einen bestimmten universellen Datentyp definieren und alle anderen Typen in diesen Typ konvertieren. Dieses Vorgehen erscheint zunächst umständlicher, da man nun zwar keine Gleichheits-Funktion für jeden Typ mehr angeben muss, dafür aber eine Konvertierungsfunktion. Bei genauerem Hinsehen zeigt sich jedoch ein Vorteil: Die Konvertierungsfunktionen kann man verwenden, um eine unbegrenzte Zahl generischer Funktionen anzuwenden. Statt viele Funktionen für viele Typen zu implementieren braucht man also nur noch eine Konvertierungsfunktion für jeden Typ und eine Implementierung für jede generische Funktion.

Avoiding quadratic number of function definitions with universal datatype
Um drei generische Funktionen für vier Datentypen zu implementieren, braucht man unter Verwendung eines universellen Datentyps nur \(4+3\) statt \(4*3\) Funktionen zu implementieren.
Es stellt sich die Frage, wie der universelle Datentyp beschaffen sein muss, um die Definition möglichst vieler generischer Funktionen zu unterstützen. Zunächst muss es möglich sein, jeden Datentyp1 injektiv in den universellen Datentyp abzubilden, da wir ansonsten keine sinnvolle Gleichheits-Funktion implementieren könnten. Darüber hinaus muss die Struktur eines Wertes erhalten bleiben, damit die Implementierung einer generischen Funktion auf dem universellen Datentyp das Muster, dem man für den Original-Datentyp folgen würde, anwenden kann.
Wir verwenden deshalb den folgenden universellen Datentyp.
data Universal
= Unit
| Pair Universal Universal
| This Universal
| That UniversalDiesen Datentyp können wir verwenden, um das Muster, dem die Gleichheits-Funktion folgt, zu formalisieren. Dazu geben wir einfach eine ==-Funktion für den Typ Universal an.
instance Eq Universal where
Unit == Unit = True
Pair u1 v1 == Pair u2 v2 = u1 == u2 && v1 == v2
This u1 == This u2 = u1 == u2
That u1 == That u2 = u1 == u2
_ == _ = FalseWir können nun Werte beliebiger Typen, die sich in den Universal-Typ konvertieren lassen, mit dieser Funktion vergleichen. Zur Konvertierung in den Universal-Typ definieren wir eine Typklasse Generic
class Generic a where
universal :: a -> Universalmit deren Hilfe wir einen generischen Gleichheits-Test implementieren können.
genericEq :: Generic a => a -> a -> Bool
genericEq x y = universal x == universal yDie Funktion universal ist selbst eine Datentyp-generische Funktion und zwar die einzige, die man für jeden Typ gesondert programmieren muss. Sie folgt einem festen Muster, welches wir im Folgenden untersuchen.
Um mehrere Konstruktoren eines Datentyps auseinander zu halten, verwendet man die Konstruktoren This und That. Zum Beispiel konvertiert man Werte vom Typ Bool wie folgt:
instance Generic Bool where
universal False = This Unit
universal True = That UnitHierbei verwenden wir Unit als Argument von This und That, da die Konstruktoren von Bool keine Argumente haben (Konstruktoren mit Argumenten widmen wir uns später). Bei Datentypen mit mehr als zwei Konstruktoren, können wir This und That geschachtelt verwenden. Beispielhaft betrachten wir die Konvertierung eines Datentyps für vier Farben.
data Colour = Red | Green | Blue | YellowIn der Generic-Instanz für Colour schachteln wir die This und That Konstruktoren so, dass man an der Anzahl der That-Konstruktoren erkennen kann, um welche Farbe es sich handelt.
instance Generic Colour where
universal Red = This Unit
universal Green = That (This Unit)
universal Blue = That (That (This Unit))
universal Yellow = That (That (That (This Unit)))Alternativ zu so einer linearen Kodierung der Farben, können wir auch eine Art Binärkodierung verwenden.
instance Generic Colour where
universal Red = This (This Unit)
universal Green = This (That Unit)
universal Blue = That (This Unit)
universal Yellow = That (That Unit)Mit dieser Kodierung ist die Anzahl der verwendeten Konstruktoren pro Regel logarithmisch in der Anzahl der Regeln statt linear.
Zur Definition der generischen universal-Funktion verwenden wir also zur Unterscheidung von \(n\) Konstruktoren eine Schachtelung von \(log(n)\) This und That Konstruktoren entsprechend der Binärdarstellung der Nummer des Konstruktors.
Wir können nun die generische Gleichheits-Funktion auf Boole'sche Werte und auf Farben anwenden, aber nicht auf einen Boole'schen Wert und eine Farbe:
ghci> genericEq False False
True
ghci> genericEq Red Blue
False
ghci> genericEq False Yellow
Couldn't match expected type `Bool'
against inferred type `Colour'Wir kommen nun zu Datentypen, deren Konstruktoren Argumente haben und definieren dazu eine Generic-Instanz für Listen.
instance Generic a => Generic [a] where
universal [] = This Unit
universal (x:xs) = That (Pair (universal x) (universal xs))Wieder unterscheiden wir die Konstruktoren mit This und That, verwenden aber zusätzlich den Pair-Konstruktor, um die Argumente von (:) zu speichern. Durch diese Definition können wir nun zum Beispiel Listen von Farben konvertieren:
ghci> universal [Red]
That (Pair (This (This Unit)) (This Unit))Im Allgemeinen verwenden wir Unit bei Konstruktoren ohne Argumente und schachteln \(n-1\) Pair-Konstruktoren bei Konstruktoren mit \(n\) Argumenten. Auch bei der Schachtelung von Pair-Konstruktoren haben wir unterschiedliche Möglichkeiten. Zum Beispiel können wir die Elemente linear oder als balancierten Baum schachteln. Die Art der Schachtelung hat aber anders als bei This und That keinen Einfluss auf die Anzahl der benötigten Pair Konstruktoren, da ein Binärbaum mit \(n\) Blättern unabhängig von seiner Struktur immer genau \(n-1\) innere Knoten hat.
Die Konstruktoren des Universal-Datentyps entsprechen genau den Konstruktoren der ()-, (,)-, und Either-Typen:
instance Generic () where
universal () = Unit
instance (Generic a, Generic b) => Generic (a,b) where
universal (x, y) = Pair (universal x) (universal y)
instance (Generic a, Generic b) => Generic (Either a b) where
universal (Left x) = This (universal x)
universal (Right y) = That (universal y)Diese Typen reichen aus, um die Strukturinformation beliebiger algebraischer Datentypen zu kodieren, denn nach dem oben erklärten Muster lassen sich alle algebraischen Datentypen in den Universal-Typ konvertieren.
Bei der Definition von Konvertierungs-Funktionen ist man nicht an das beschriebene Muster gebunden, es stellt nur eine mögliche Art dar, beliebige Datentypen zu konvertieren. Zum Beispiel können wir Listen auch konvertieren, ohne This und That zu verwenden:
instance Generic a => Generic [a] where
universal [] = Unit
universal (x:xs) = Pair (universal x) (universal xs)Diese Definition führt zu einer kompakteren Darstellung von Listen:
ghci> universal [Red]
Pair (This (This Unit)) UnitBei eigenen Konvertierungs-Funktionen müssen wir sicherstellen, dass diese injektiv sind, das heißt, dass keine unterschiedlichen Werte des Original-Typs auf den selben Wert des Universal-Typs abgebildet werden. Weiterhin sollte die Strukturinformation bei der Konvertierung vollständig erhalten bleiben. Beides ist mit Konvertierungs-Funktionen, die nach dem generischen Muster erstellt werden, der Fall.
Ein weiteres Beispiel für eine generische Haskell-Funktion ist die show-Funktion zum Umwandeln eines Wertes in einen String. Auch diese Funktion kann man generisch über die Struktur des Arguments definieren. Die im Universal-Typ gespeicherte Struktur-Information reicht zur Definition von show aber nicht aus. Es fehlt die Information über die Konstruktor-Namen, die im erzeugten String vorkommen.
Es ist möglich, den Universal-Typ um weitere Informationen zu erweitern, auch um solche, mit deren Hilfe wir show implementieren könnten. Wir beschränken uns aber auf den gezeigten Universal-Datentyp und definieren anstelle von show eine generische Funktion serialize, die einen beliebigen Datentyp in eine Bitfolge übersetzt:
serialize :: Generic a => a -> [Bool]
serialize = binary . universalbinary ist dabei eine Funktion, die einen Universal-Wert in eine Liste Boole'scher Werte übersetzt.
binary :: Universal -> [Bool]
binary Unit = [False,False]
binary (Pair u v) = [False,True ] ++ binary u ++ binary v
binary (This u) = [True ,False] ++ binary u
binary (That u) = [True ,True ] ++ binary uDa der Universal-Typ vier Konstruktoren hat, verwenden wir zwei Bits für jeden und serialisieren sie von links nach rechts. Hier ein Beispielaufruf:
ghci> binary (Pair (That Unit) Unit)
[False,True,True,True,False,False,False,False]Dadurch, dass wir die binary-Funktionion für den Universal-Typ definiert haben, können wir beliebige Daten, deren Typ eine Instanz der Klasse Generic ist, in Bitfolgen transformieren.
ghci> serialize False
[True,False,False,False]
ghci> serialize [()]
[False,True,False,False,False,False]Wie man sieht, verwendet diese Implementierung mehr Bits als man erwarten könnte. Zum Beispiel kann man Boole'sche Werte mit einem einzigen Bit kodieren satt wie hier mit vieren. Gelegentlich ist eine generische Implementierung mittels des universellen Datentyps weniger effizient als eine auf einen bestimmten Datentyp spezialisierte Implementierung.
Die erzeugten Bitfolgen lassen sich auf eindeutige Weise in den Universal-Datentyp zurück übersetzen. Zusammen mit einer Funktion, die Universal-Werte in beliebige Datentypen zurück konvertiert, kann man also auch eine Funktion deserialize schreiben, die Daten aus einer Bitfolge einliest (Übung).
Zum Abschluss dieses Kapitels implementieren wir eine generische Trie-Struktur, die man mit Schlüsseln beliebigen (nach Universal konvertierbaren) Typs verwenden kann. Dazu definieren wir zunächst einen Trie für den Universal-Typ nach dem im vorigen Kapitel diskutierten Muster.
data UniMap a = UniMap (Maybe a)
(UniMap (UniMap a))
(UniMap a)
(UniMap a)Die Definitionen der empty-, lookup- und update-Funktionen sind im bereitgestellten Generic-Modul verfügbar. Aufbauend auf dieser Implementierung definieren wir Zugriffsfunktionen für beliebige Datentypen, hier am Beispiel der lookup-Funktion:
lookupG :: Generic k => k -> UniMap a -> Maybe a
lookupG = lookupUni . universalMit solchen Zugriffsfunktionen können wir in eine emptyUniMap Werte zu beliebigen Schlüsseln eintragen.
ghci> let m = insertG [True,False] 42 emptyUniMap
ghci> lookupG [True,False] m
Just 42
ghci> lookupG [False] m
Nothing
ghci> lookupG True m
NothingDer letzte Aufruf ist verdächtig. Obwohl wir m mit Schlüsseln vom Typ [Bool] verwendet haben, können wir sie auch mit anderen Schlüssel-Typen, die eine Generic-Instanz sind, verwenden. Das ist eine potentielle Fehlerquelle, denn obwohl es in diesem Beispiel richtig ist, dass kein Wert unter dem Schlüssel True abgelegt wurde, ist nicht sichergestellt, dass unterschiedliche Werte unterschiedlicher Typen verschiedene Universal-Darstellungen haben. Die Konvertierungsfunktionen sind nur injektiv bezüglich eines bestimmten Typs, nicht über Typgrenzen hinweg.
Wir definieren deshalb einen Trie für generische Werte, bei dem jeder einzelne Trie mit nur einem Schlüsseltyp (verschiedene Tries aber mit unterschiedlichen Schlüsseltypen) verwendet werden können.
newtype GenMap k a = GenMap (UniMap a)GenMap ist im Wesentlichen nur ein neuer Name für UniMap mit einer wichtigen Besonderheit: Der GenMap Typkonstruktor hat einen zusätzlichen Parameter k für den Schlüsseltyp. Dieser Parameter ist ein sogenannter Phantom-Typ, da er auf der rechten Seite der Definition nicht vorkommt. Wir verwenden ihn in den Typsignaturen der Zugriffsfunktionen für GenMaps, um sicher zu stellen, dass mit einer gegebenen GenMap immer Schlüssel desselben Typs verwendet werden.
Die Implementierung der Zugriffsfunktionen für GenMaps greift auf die für UniMaps zurück, verwendet aber restriktivere Typsignaturen (hier am Beispiel von lookupGen):
lookupGen :: Generic k => k -> GenMap k a -> Maybe a
lookupGen k (GenMap m) = lookupUni (universal k) mDadurch, dass der Typparameter k im ersten und zweiten Argument von lookupGen identisch ist, können wir nur mit Schlüsseln eines einzigen Typs auf eine bestimmte GenMap zugreifen.
Wir können GenMaps ähnlich verwenden wie im obigen Beispiel. Sobald wir aber eine Zugriffsfunktion auf einer GenMap mit einem konkreten Schlüssel ausgeführt haben, ist der Typ der GenMap auf diesen Schlüsseltyp festgelegt.
ghci> let m = insertGen [True,False] 42 emptyGenMap
ghci> lookupGen [True,False] m
Just 42
ghci> lookupGen [False] m
Nothing
ghci> lookupGen True m
Couldn't match expected type `Bool'
against inferred type `[Bool]'
ghci> :t m
m :: GenMap [Bool] IntDer lookupGen Aufruf mit einem Bool-Schlüssel führt zu einem Typfehler, da vorher mit einem Schlüssel vom Typ [Bool] auf m zugegriffen wurde. Auf eine neue GenMap können wir mit Bool-Schlüsseln zugreifen:
ghci> let m = insertGen True 42 emptyGenMap
ghci> :t m
m :: GenMap Bool Int
ghci> lookupGen True m
Just 42Wir haben durch Phatom-Typen erreicht, dass auf eine GenMap nur mit Schlüsseln eines Typs zugegriffen werden kann. Die erste Zugriffsfunktion legt dabei den Schlüsseltyp fest und stellt dadurch sicher, dass sich gleich dargestellte Schlüssel unterschiedlicher Typen nicht in die Quere kommen.
Wir vernachlässigen hierbei primitive Datentypen wie Int oder Char und beschränken uns auf selbst definierte, algebraische Datentypen (ohne Funktionen).↩